Understanding Why MAML Can Adapt Fast

When MAML Can Adapt Fast and How to Assist When It Cannot

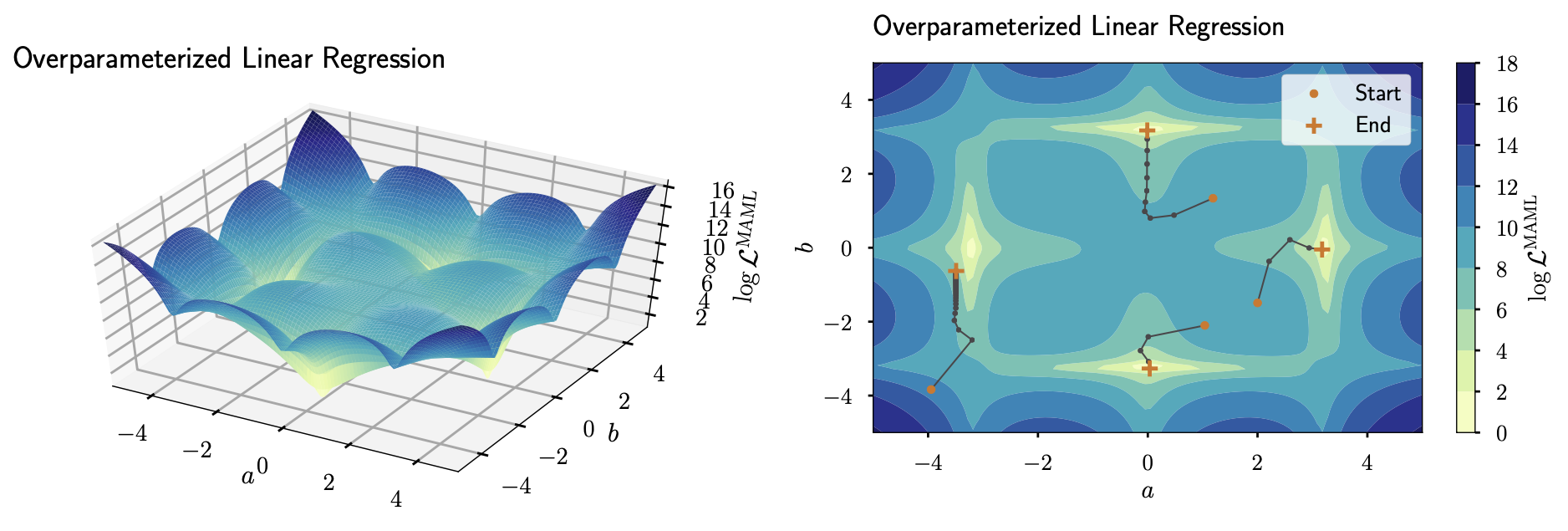
Loss surface and trajectories of MAML-trained deep linear models.

Abstract

Model-Agnostic Meta-Learning (MAML) and its variants have achieved success in meta-learning tasks on many datasets and settings. Nonetheless, we have just started to understand and analyze how they are able to adapt fast to new tasks. In this work, we contribute by conducting a series of empirical and theoretical studies, and discover several interesting, previously unknown properties of the algorithm. First, we find MAML adapts better with a deep architecture even if the tasks need only a shallow one. Secondly, linear layers can be added to the output layers of a shallower model to increase the depth without altering the modelling capacity, leading to improved performance in adaptation. Alternatively, an external and separate neural network meta-optimizer can also be used to transform the gradient updates of a smaller model so as to obtain improved performances in adaptation. Drawing from these evidences, we theorize that for a deep neural network to meta-learn well, the upper layers must transform the gradients of the bottom layers as if the upper layers were an external meta-optimizer, operating on a smaller network that is composed of the bottom layers.

Illustrative Results

As a small teaser, the following figure illustrates a simple failure-mode of MAML: although the black and red models have the same modelling capacity, only the overparameterized one is able to adapt quickly.

Why? Please refer to our paper for detailed explanations, including theoretical results and empirical analysis on Omniglot, CIFAR-FS, and mini-ImageNet.

We also introduce several methods that improve the adaptability of gradient-based meta-learning algorithms such as MAML and ANIL; one is to add additional linear layers, the other to learn an external meta-optimizer.

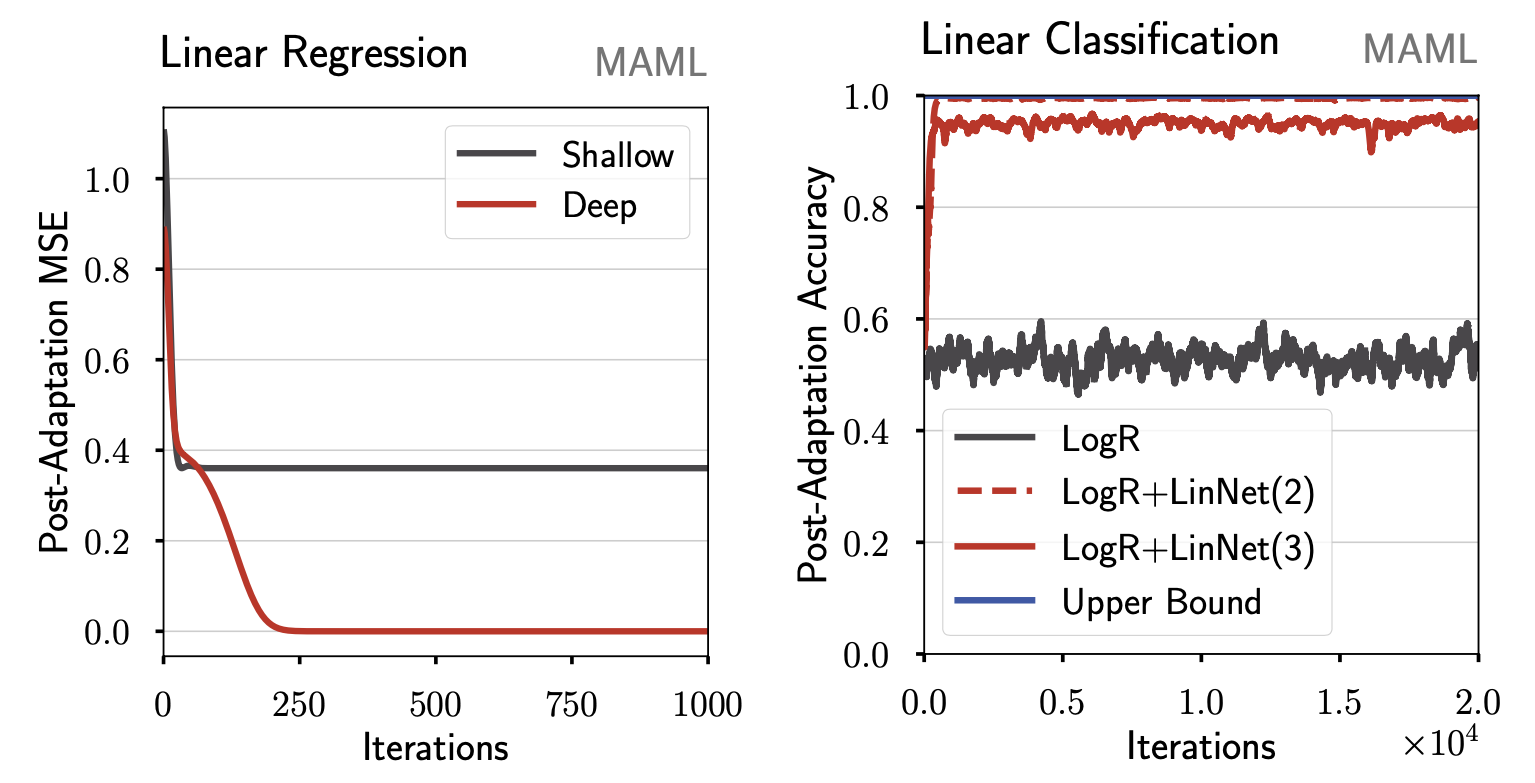
MAML fails to adapt quickly with shallow linear models (Shallow, LogR) on simple convex tasks – here, linear regression and binary classification. Overparameterizing the models with extra parameters (Deep, LogR+LinNet) lets MAML meta-learn optimization weights that enable fast-adaptation.

Code

The implementation of our meta-optimizer, Meta-KFO, as well as all baselines are available in learn2learn. We also release example implementations of Meta-KFO, available at:

import torch
import learn2learn as l2l

model = MyModel()
metaopt = l2l.optim.KroneckerTransform(l2l.nn.KroneckerLinear)
gbml = l2l.algorithms.GBML(
    module=model,
    transform=metaopt,
    lr=0.01,
    adapt_transform=True,
)
opt = torch.optim.SGD(gbml.parameters(), lr=0.001)

for iteration in range(10):
    opt.zero_grad()
    task_model = gbml.clone()
    loss = compute_loss(task_model)
    task_model.adapt(loss)
    loss = compute_loss(task_model)
    loss.backward()
    opt.step()

Reference

Please cite this work as

S. M. R. Arnold, S. Iqbal, F. Sha, When MAML Can Adapt Fast and How to Assist When It Cannot. AISTATS 2021.

or using the following BibTex entry.

@InProceedings{pmlr-v130-arnold21a,
  title =    { When MAML Can Adapt Fast and How to Assist When It Cannot },
  author =       {Arnold, S{\'e}bastien M. R. and Iqbal, Shariq and Sha, Fei},
  booktitle =    {Proceedings of The 24th International Conference on Artificial Intelligence and Statistics},
  pages =    {244--252},
  year =     {2021},
  editor =   {Banerjee, Arindam and Fukumizu, Kenji},
  volume =   {130},
  series =   {Proceedings of Machine Learning Research},
  month =    {13--15 Apr},
  publisher =    {PMLR},
  pdf =      {http://proceedings.mlr.press/v130/arnold21a/arnold21a.pdf},
  url =      {http://proceedings.mlr.press/v130/arnold21a.html},
}

Contact
Séb Arnold - seb.arnold@usc.edu