Autograd: automatic differentiation

Central to all neural networks in PyTorch is the autograd package. Let’s first briefly visit this, and we will then go to training our first neural network.

The autograd package provides automatic differentiation for all operations on Tensors. It is a define-by-run framework, which means that your backprop is defined by how your code is run, and that every single iteration can be different.

Let us see this in more simple terms with some examples.

Variable

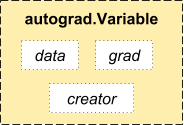
autograd.Variable is the central class of the package. It wraps a Tensor, and supports nearly all of operations defined on it. Once you finish your computation you can call .backward() and have all the gradients computed automatically.

You can access the raw tensor through the .data attribute, while the gradient w.r.t. this variable is accumulated into .grad.

Variable

There’s one more class which is very important for autograd implementation - a Function.

Variable and Function are interconnected and build up an acyclic graph, that encodes a complete history of computation. Each variable has a .grad_fn attribute that references a Function that has created the Variable (except for Variables created by the user - their grad_fn is None).

If you want to compute the derivatives, you can call .backward() on a Variable. If Variable is a scalar (i.e. it holds a one element data), you don’t need to specify any arguments to backward(), however if it has more elements, you need to specify a grad_output argument that is a tensor of matching shape.

import torch
from torch.autograd import Variable

Create a variable:

x = Variable(torch.ones(2, 2), requires_grad=True)
print(x)

Do an operation of variable:

y = x + 2
print(y)

y was created as a result of an operation, so it has a grad_fn.

print(y.grad_fn)

Do more operations on y

z = y * y * 3
out = z.mean()

print(z, out)

Gradients

let’s backprop now out.backward() is equivalent to doing out.backward(torch.Tensor([1.0]))

out.backward()

print gradients d(out)/dx

print(x.grad)

You should have got a matrix of 4.5. Let’s call the out Variable “\(o\)”. We have that \(o = \frac{1}{4}\sum_i z_i\), \(z_i = 3(x_i+2)^2\) and \(z_i\bigr\rvert_{x_i=1} = 27\). Therefore, \(\frac{\partial o}{\partial x_i} = \frac{3}{2}(x_i+2)\), hence \(\frac{\partial o}{\partial x_i}\bigr\rvert_{x_i=1} = \frac{9}{2} = 4.5\).

You can do many crazy things with autograd!

x = torch.randn(3)
x = Variable(x, requires_grad=True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

print(y)

gradients = torch.FloatTensor([0.1, 1.0, 0.0001])
y.backward(gradients)

print(x.grad)

Read Later:

Documentation of Variable and Function is at http://pytorch.org/docs/autograd

Total running time of the script: ( 0 minutes 0.000 seconds)